球の体積の求め方 公式と計算例 Scipursuit 体積の求め方 球 球の体積を求める公式は、次の通りです。 V = 4 3πr3 ここで、V は球の体積、r は球 中学数学球の体積の求め方の公式を1発で覚 「球の体積の公式」を暗記する方法を伝授しよう。 3分の4球体の24金の体積を求めるのに使用しました。 1034 女/歳代/主婦/役に立った/ 使用目的 受験する看護学校過去問に球の体積を求める問題があり、公式を度忘れしていたので活用。 0136 男/30歳代/その他/少し役に立った/ 使用目的 @ ̑̐ρE \ ʐς̌ ̂ Ƃ ؖ ́C Z wIII i 3 j Ŕ ϕ p čs 邪 C ܂łɂ o ꂷ ʂ C ̑̐ρE \ ʐς̌ ͏ w Z ̓ Ɋo Ă Ƃ悢 D m ̑̐ρn
立体 の 表面積 求め 方
球体の体積の求め方 公式
球体の体積の求め方 公式-よって公式通りの結果になりました。 では最後に楕円の体積を求めてみましょう。 これは楕円の面積を求めた方法と手順は同じで、もう既に手法は紹介し尽くしているので結構簡単に結果を導くことができます。 楕円体の体積 楕円体 円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!←今回の記事




球の表面積
球の体積の求め方 半径rの球の体積を求める公式は、次のようになります。 πは円周率(=)です。 球の体積は、半径rの3乗に比例していくということですね! (例題) 半径5cmの球の体積は? 公式にr=5を代入して球の表面積の求め方 公式と計算例 Scipursuit 表面積の求め方 球 球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。 球の表面積を求めるには、この公式に球の半径 r を代入球体 体積 求め 方もくじ 1 球の体積を出す公式での求め方 11 円柱と球の体積の関係;円すい(円錐)の体積の求め方と問題 図形の面積(体積)や周りの長さを文字式にする問題まとめ 補足 上の練習問題で、半径が2cmの球は半径が1cmの球に比べて、体積は8倍
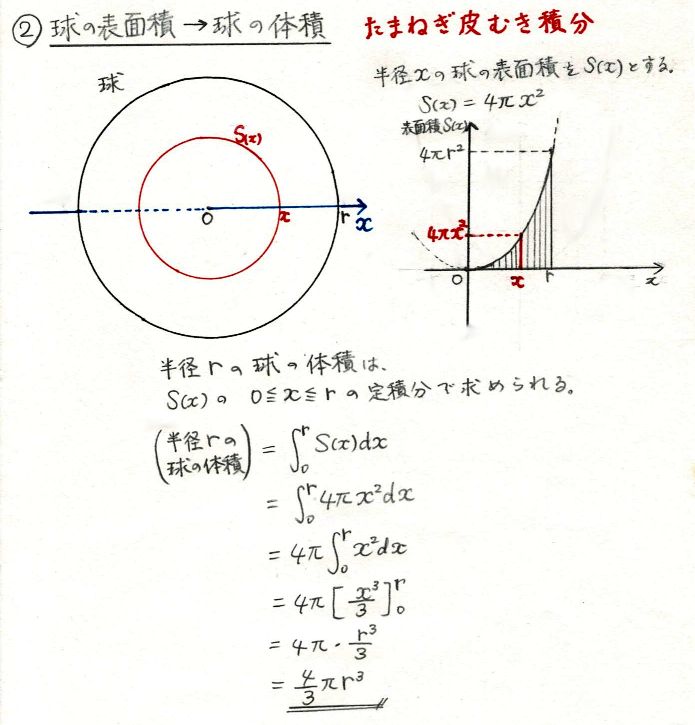
①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 -x 2) であるから、円の面積は、S(x)=π(r 2 -x 2) となる。 よって、球の体積V この公式の応用例として,1辺が a a a の正四面体の内接球の半径を求めてみます。入試問題で頻出です。 正四面体の表面積と体積は公式として覚えておくとよいでしょう。 →正三角形の面積,正四面体の体積の体積を求めた。私は特に上が閉じた形を直観的に洋傘と呼ぶ。 これは関が9 と呼んだ立体に相当し、 これに中錐に相当する 体積を加えれば球欠の体積が得られる (右の下図) $\text{。}7$ 節で引
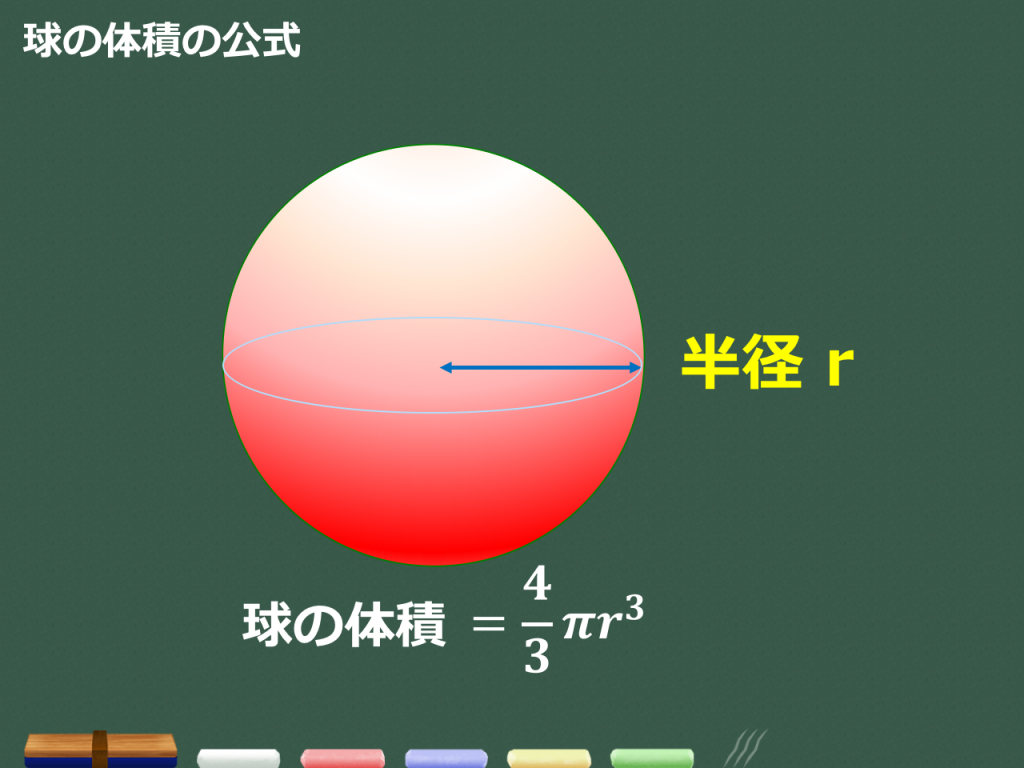
四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 よって公式通りの結果になりました。 では最後に楕円の体積を求めてみましょう。 これは楕円の面積を求めた方法と手順は同じで、もう既に手法は紹介し尽くしているので結構簡単に結果を導くことができます。 楕円体の体積 楕円体半径 (はんけい) r の球の体積は、次の式で求められます。 球 (きゅう) の体積 \begin{align*} V = \frac{4}{3}\pi r^3 \end{align*} 体積 = 4 × 314 × 半径 × 半径 × 半径 ÷ 3 公式の 導出 (どうしゅつ) 方法と計算例は、「球の体積の求め方」をご覧ください。




中1 数学 空間図形14 球 6分 Youtube




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半 円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。ただし体積の求め方 計算公式一覧 Scipurusit 半径 (はんけい) r の球の体積は、次の式で求められます。 球 (きゅう) の体積 \begin{align*} V = \frac{4}{3}\pi r^3 \end{align*} 体積 = 4 × 314 × 半径 × 半径 × 半径 ÷ 3 公式の 導出 (どうしゅつ) 方法と計算例は、「球の体積の




球の表面積と体積の公式 数学fun




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張
V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin 球の体積の求め方でなぜ3分の4が出てくるのかわかりません。 中1でもわかるように説明お願いします (>人<;) 縮め る球の表面積と体積 解く前に確認しよう ④ 球の表面積 半径が7の球の表面積をねとすると ぐー477" ④ 球の体積 半径が7の球の体積をしと球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) いちいち半径の公式から換算するのは能率が悪い。 円と球の公式



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ



19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求め 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、 3分の4 × 円周率 × 半径 × 半径 × 半径 ってことだね。 この公式でどんなボールの体積も計算できちゃうんだ。 なお, r 1 = 0 r_1=0 r 1 = 0 または r 2 = 0 r_2=0 r 2 = 0 とすることで球欠の体積公式: V = 1 6 π h (3 r 2 h 2) V=\dfrac{1}{6}\pi h(3r^2h^2) V = 6 1 πh (3 r 2 h 2) が得られます。



球の体積と玉率 雑学のソムリエ




体積の求め方 計算公式一覧
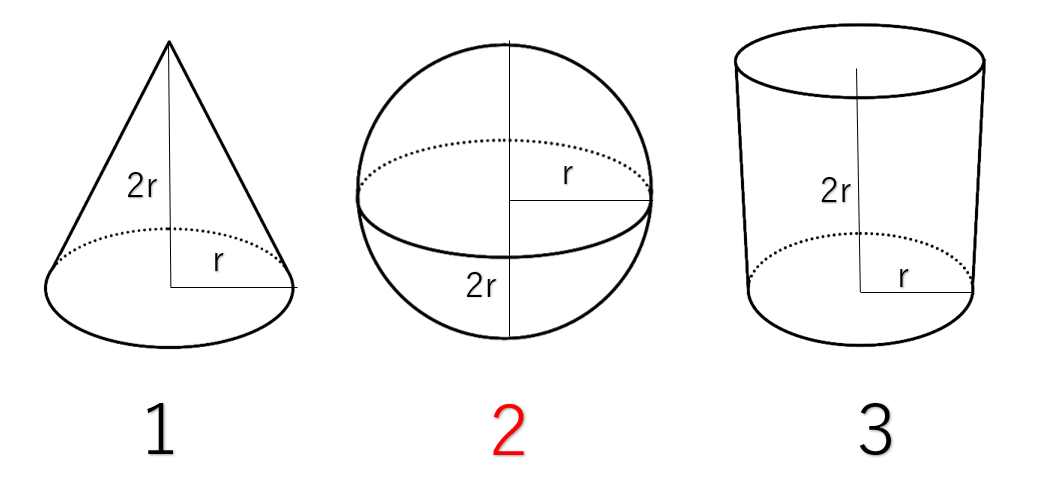
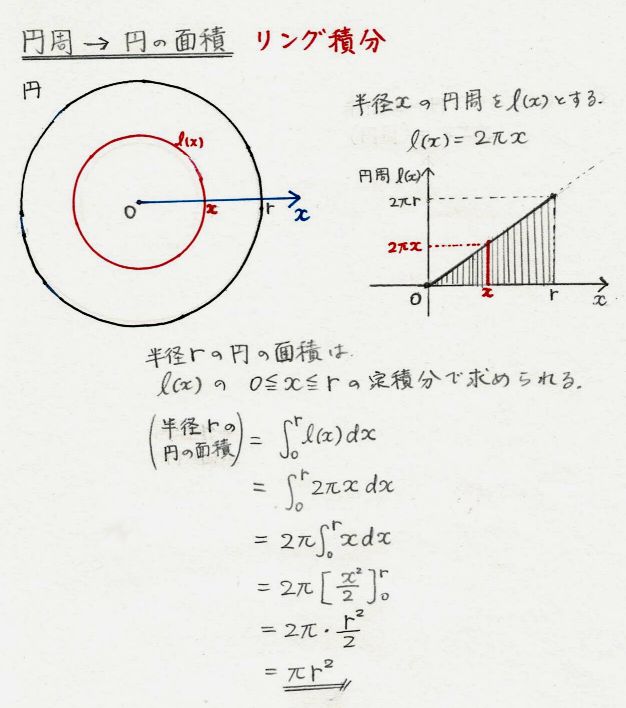
輪切りの考え方から, 球体の表面積=円柱の側面積 ∴ 球体の表面積=円柱の側面積= 4πr2立方体・直方体の体積の求め方|小学生に教えるための分かりやすい解説 管理人 9月 , 18 / 12月 1, 18 立体の体積という新しい分野なだけに、なかなかイメージしづらかったり、理解しづらい子は円柱の体積を求める公式は、 V = Sh = πr^2 h で表されます。このページでは、例題と共に、円柱の体積を計算する方法を説明しています。また、斜円柱の体積の求め方も説明しています。




球の表面積と体積の公式 数学fun



立体 の 表面積 求め 方
まず、ボール全体の体積を求め、それを半分にすることで、水中にある分の体積が求められます。球体の体積は (4/3)π(半径) 3 で求められるので、 (4/3)π(05) 3 = 0524 m 3 であることがわかります。それを半分にするので、 0524/2 = 0262 m 3 が水中にある体積です。 簡単公式3分でわかる!半球の体積の求め方 半球の体積の求め方に公式はあるの?? こんにちは!この記事をかいているKenだよ。シャツほしいね。 半球の体積を求め方 には公式があるよ。 半径rの半球の体積は、 (3分の2π) × (rの3乗) になるんだ 体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱(管) 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方




球体の体積 中学生に分かるように真剣に考えてみた うちーノート




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館
球の体積と表面積の公式 半径 r r r の球の表面積は S = 4 π r 2 , S=4\pi r^2,\ S = 4 π r 2 , 球の体積は V = 4 3 π r 3 V=\dfrac{4}{3}\pi r^3 V = 3 4 π r 3 である。球の体積の求め方 大学数学 Volume of a sphere 球体の体積積分で求める方法 うちーノート 中学数学球の体積の求め方の公式を1発で覚 球の体積の求め方の公式が覚えられねえ!! こんにちは!この記事をかいているKenだよ。ビニール傘を買っ球の体積の求め方 公式と計算例 Scipursuit 体積の求め方 球 球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。 球の体積を求めるには、この公式に球の半径 r を代入すればよいだけです。 このページの続きでは、例題を使って、この公式の使い方を説明しています。



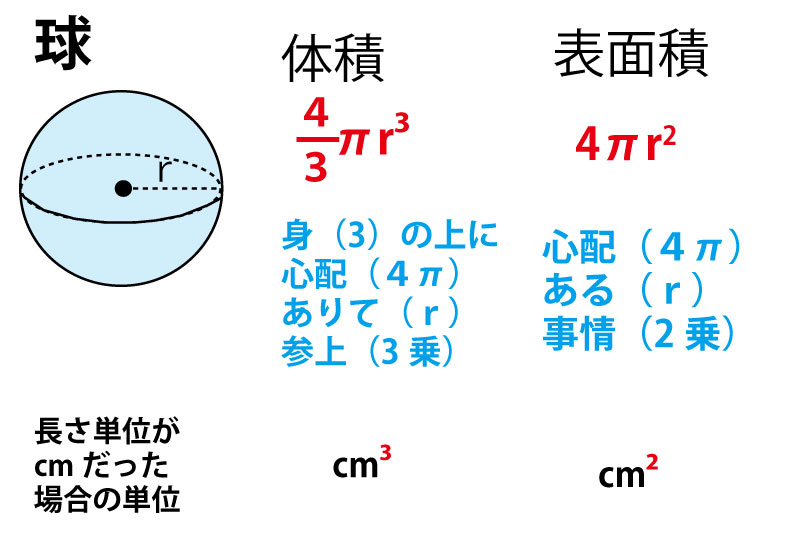
球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




面積 体積 計算ツール 福井鋲螺株式会社 冷間鍛造 冷間圧造 ヘッダー加工の専門メーカー リベット 特殊形状パーツおよび省力機器の製造 販売
壮大 球体 の 体積 の 求め 方 公式 球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを 1:球の体積の求め方(公式) まずは球の体積の求め方(公式)を紹介します。 下の図のように、 半径rの球があるとき、球の体積は4πr 3 / 3 となります。 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず! 球の表面積の公式を暗記するため




球の体積 球の表面積の公式の導出 積分 優技録




球の体積と表面積 公式と計算問題と証明 Irohabook



2



球の表面積の公式の求め方




球の表面積と体積の公式 数学fun




球の表面積の求め方 公式と計算例




2次元 3次元 4次元 5次元 高次元 の球の体積 宇宙に入ったカマキリ




球の体積 球の表面積の公式の導出 積分 優技録



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



中1 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




球の表面積
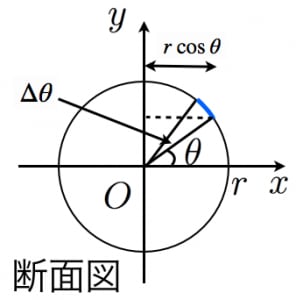



球の体積と表面積を積分で証明 高校数学の美しい物語




球の表面積と体積の公式 数学fun




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



1




中1数学 球 例題編 映像授業のtry It トライイット



至急 球を4等分したものの体積と表面積の求め方をを教えてください Yahoo 知恵袋



この画像は半径6 の球を 中心を通る平面で4等分してできた立体のうちの一 Yahoo 知恵袋




球の体積と表面積 Youtube



1




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ



大学入試問題




球の体積の公式 求め方や覚え方のコツを紹介するよ 中学や高校の数学の計算問題




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



研究



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ



3




球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



数学トピックq A




スタディピア 立体の表面積




この球体の体積の求め方を教えてください それと私は数学の公式をすぐに忘れてしまうので Clear



球の表面積の公式の求め方




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球の体積 高精度計算サイト




円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ




球の表面積と体積の公式 数学fun




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球の体積の求め方 公式の覚え方と計算方法まとめ 中学数学 理科の学習まとめサイト




角柱 円柱の表面積と体積の公式 数学fun



1




中1 数学 6 5 球の体積 表面積 Youtube




球の体積の求め方 感じる科学 味わう数学




Mathematics 球の体積と表面積を求める公式 働きアリ




球の体積の公式を積分を使わず導く 中受でも出るかも 兄中学生活




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ
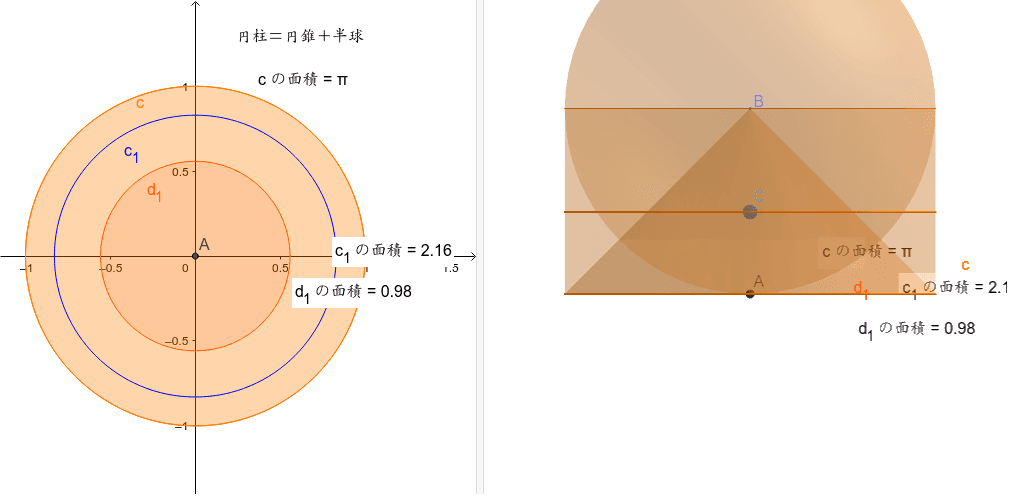



球の体積の求め方 Geogebra




中学数学 空間図形 体積の問題のコツ




球の表面積 体積 身勝手な主張



球の表面積と体積の求め方 苦手な数学を簡単に




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく




中1 中一数学 球の表面積と体積 中学生 数学のノート Clear




球の表面積の公式について みたにっき はてな



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ



球の体積 簡単に計算できる電卓サイト




中1数学 球 練習編 映像授業のtry It トライイット




球の体積 表面積の求め方 公式 小学生 中学生の勉強




球の表面積と体積を求める方法 中学数学 By じょばんに マナペディア
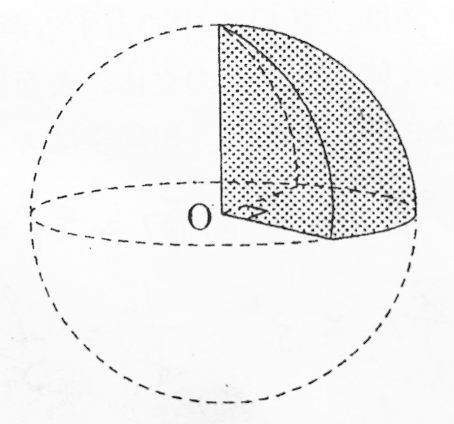



球の問題 苦手な数学を簡単に




中1 数学 中1 84 球について Youtube




曲面 番外編 曲面の面積 身勝手な主張




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ
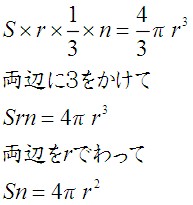



Mathematics 球の体積と表面積を求める公式 働きアリ



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



球の体積の求め方とその証明 高等学校で学ぶ積分の知識が必要




半球の体積と表面積を計算する 具体例で学ぶ数学




角錐 円錐の体積と表面積の公式 数学fun



Studydoctor球の表面積や体積の公式と求め方 中学1年数学 Studydoctor




中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear




球の体積と表面積 Jsciencer




球冠 Wikipedia




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾
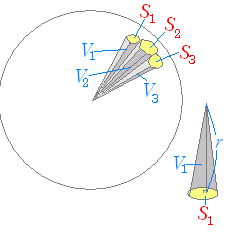



例題対比 球の体積と表面積




中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su
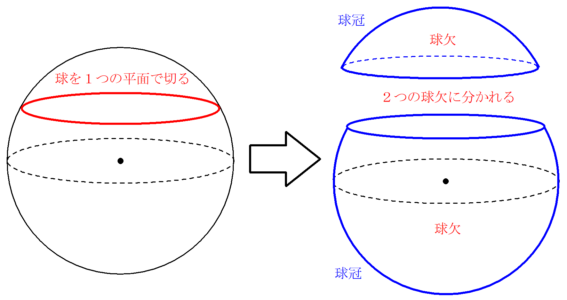



球欠と球冠 Fukusukeの数学めも




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




2 を教えてください Clear




中1数学 空間図形 球の体積の求め方 Youtube




球の体積公式の微分が表面積になっている理由 Youtube



0 件のコメント:
コメントを投稿