第3学年 1 式の展開と因数分解 知識・技能の習得を図る問題解答 年 組 号氏名 練習問題② 1 (1) (x +9)2 ポイント =x 2+18x +81 公式 (a + b )2=a 2+2ab + b 2 を利用しよう。 x をa,9を b と考え,公式にあてはめると, 1 x 2 x2となるね。多項式 中学数学単項式と多項式の乗除 中学数学多項式と多項式の乗除 中学数学式の展開 乗法公式 中学数学因数分解・共通因数でくくる 中学数学因数分解・乗法公式乗法公式とは 式を展開するときに、次の公式がよく用いられます。 これらの公式乗法公式とよばれる公式です、 後の 因数分解 という単元でとても大切になるので、必ず覚える ようにしましょう。 覚えるためには、たくさんの問題を解くしかありません。

深圳高中数学选修2 3二项式定理知识点总结归纳 深圳学而思1对1
展開 公式 中学
展開 公式 中学-展開の公式応用編1: 看護学校の受験数学 (中学数学)を分かりやすく図解で説明 展開の公式応用編1: 看護学校の受験数学 (中学数学)を分かりやすく図解で説明 どうしても入試問題になると 「解けない! ! 」 なんてこともよく聞きます。 が出題され型の式を、乗法公式 を用いて展開するこ とができる。 分配法則や交換法則 及び乗法公式を活用 して、いろいろな計算 をすることができる。 多項式の共通な因数 をくくり出す因数分 解ができる。 乗法公式1を基にす る因数分解ができる。



资料分析 二项展开式法 事业单位招聘考试网
= 1000 22・2・ ← 「展開公式(xa) 2 = x 22axa 2 」 = = // (2) 1002 2 = () 2 = 1000 2 2・2・ = = // (3) 1016×984 = ()() ← 「展開公式 (xa)(xa) = x 2a 2 」 = 2(a2)(b1) = aba2b2 展開の基本は分配法則である。 先に公式を暗記するより、まずは分配法則をつかって確実に展開できるようになってから公式を覚えたほうが上達も早く、応用にもつよくなる。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru
緑 桃 == 展開公式の応用問題 == 問題1 次の各式において空欄に入る値を下の選択肢から選んでください.(正しいものをクリック) (※暗算ではできません.各自計算用紙で計算してから選択肢を選んでください) (1) (abc) 2 (bc−a) 2 (ca−b) 2 (a 中学1年生のときに基本的な分配法則を学習して、中学2年生でもう少し複雑な形を、そして中学3年生ではよく使う展開公式を学習します。 単純な計算問題だけでなく、関数や図形の問題にも式の展開の必要な場面が多くありますね。 高校でも欠かせない基礎と言えるでしょう。 中学1年 2 (X3) = (2)×X (2)× (3) =2X6 中学2年 (9ab3a12)÷3 次の式を展開しなさい。 (x2) (x4) (x3) (x3) (x3)^2 (x6)^2 解説&答えはこちら \begin {eqnarray} (x2) (x4)&=&x^2 (24)x8\\ 5pt&=&x^22x8 \end {eqnarray} \begin {eqnarray} (x3) (x3)&=&x^23^2\\ 5pt&=&x^29\end {eqnarray} \begin {eqnarray} (x3)^2&=&x^22\times x\times 33^2\\ 5pt&=&x^26x9 \end {eqnarray}
基本的な乗法公式(展開公式) I (ab)2=a22abb2 II (a−b)2=a2−2abb2 III (ab) (a−b)=a2−b2 ※ これらの公式のうち I~ IVは中学校の復習となっているが,高校の数学 I でもう一度出てくる.公式は中学校と同じでも,扱い方が少し変るところがある.例えば,これらの公式を使った置き換えによる展開,因数分解などは普通に出てくる. (証明) I ← 「総当たり中学3年の式の計算では文字式の展開公式がありますが、覚えなくて良い公式と覚えた方が良い公式があります。 展開は公式がなくてもできますが、公式が使えるものは使った方が断然早いです。 公式は「覚えて使う」で良いのですが、 展開においては公式利用とそうでないものの見分けを出来るようになると意味なく覚えることが減ります。 覚えなくて良い展開公式展開公式や因数分解を利用した代入問題のポイントと対称式や基本対称式の利用方法です。 中学3年で問題になるのは数学の便利さを利用するものです。 代入問題をやみくもに計算する算数の延長ではなく、覚えるまで練習してきた展開公式
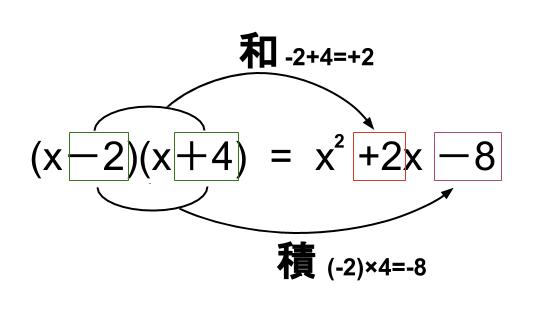



中学数学 式の展開 乗法公式 中学数学の無料オンライン学習サイトchu Su



19黑龙江大庆第十中学高二下学期第二次月考二项式定理 哔哩哔哩 つロ干杯 Bilibili
展開(おきかえ) 中学・学習サイト 中3数学式の展開(乗法公式) レベル別プリン3つの対称な変数が現れる展開公式 ( x a) ( x b) ( x c) = x 3 ( a b c) x 2 ( a b b c c a) x a b c (xa) (xb) (xc)\\=x^3 (abc)x^2 (abbcca)xabc (xa)(x b)(x c) = x3 (a b c)x2 (abbc ca)xabc ( a b c) ( a 2 b 2 c 2 − a b − b c − c a) = a 3 b 3 c 3 − 3 a b c ここまで紹介した展開公式は、(2x3)(3x4)の様な式では使えない。 カッコの中の前部分が異なるからだ。 (2x +5)(2x +1) ←展開公式が使える (2x -3)(3x -4) ←展開公式が使えない よって(2x-3)(3x-4) は分配法則を使って展開する必要がある。 一応解答を書いて




乗法公式の問題 a b a b の展開を練習しよう 中学や高校の数学の計算問題




二项式定理常见的解题策略 简书
公式を使って,展開・因数分解をしたり,素因数分解とそれを用いて約数を調べることが出来たりする 式の展開・因数分解,素因数分解の意味や文字を用いて数や図形の性質を説明する方法を理解する 本時の目標 多項式 (xa)(xb) ( x a) ( x b) を展開するA+bをXとおこう a+b=Xとおくと (X-c) 2 これなら公式を使って展開できるよね。 (X-c) 2 =X 2 -2cX+c 2 ただし、 Xはa+bに戻す 必要があるから、 (a+b) 2 -2c(a+b)+c 2 として計算しよう。 ①の答え数日間に渡り展開の基礎・応用と説明してきましたが、 理解できましたか? 中学数学に限りらず、高校数学でも展開の公式は100%使うので この機会に覚えておいてください。 当看護予備校でも、学生様の皆様には、 まず、展開の問題の説明から丁寧にしていくのですが、 社会人の皆




函数y 2 X的几种幂级数展开 百度经验



泰勒展开定理 西瓜视频搜索
B×c+b×d これを合わせて (a+b)(c+d) =a×c+a×d+b×c+b×d = ac+ad+bc+bd となるんだ。 カッコを開くことを 展開 と呼ぶんだけど、 (a+b)(c+d)の展開の公式はめっちゃくっちゃ重要だから、絶対に覚えるようにしよう。
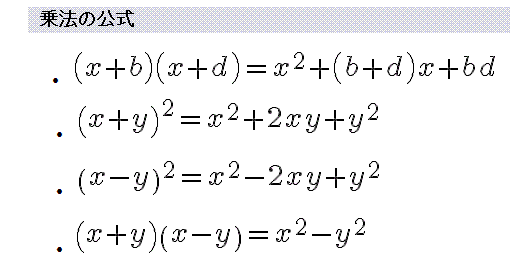



Lt Div Gt 中学生数学公式




一元函数求极限问题的处理方法及典型例题分析 泰勒 习题 展开式 网易订阅




深圳高中数学选修2 3二项式定理知识点总结归纳 深圳学而思1对1



乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係



高中数学 二项式定理 笔记 维生素 高中数学 教育 中学教育




二項式係數 维基百科 自由的百科全书



展開公式




排列组合的基本理论和公式 百度文库




展開公式のまとめ 中学生や高校生の子はぜひ覚えておきたい 中学や高校の数学の計算問題




二项式展开式系数和 搜狗搜索



云南省曲靖市第二中学届高三上学期第四次周考数学 理 试题含答案 淘文库




数以兴焉app 数以兴焉下载 数以兴焉官方21免费下载安装
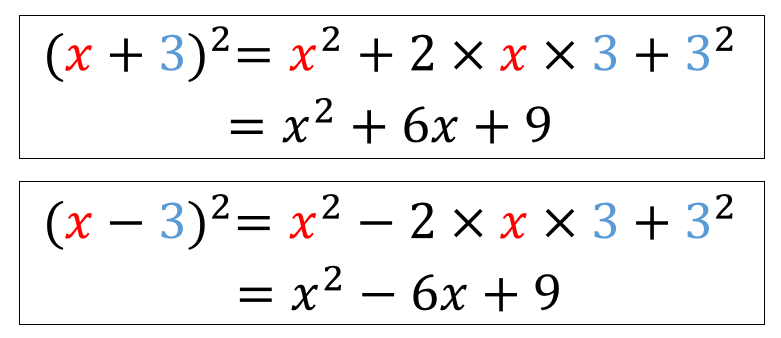



中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ




常用泰勒展开 每天的学习笔记 Csdn博客 泰勒公式展开式大全



班主任在校打学生 雷式中学 基本属实 已展开调查 腾讯新闻




幂级数展开公式 冷月无声的博客 Csdn博客 幂级数展开式




Arcsinx的泰勒展开式 Arcsinx在x 0点的局部泰勒公式怎么求 三人行教育网 Www 3rxing Org



方程的求根公式和根的展开式及其算法 Cnki学问



Ok 大学视角下的中学数学 泰勒展开 Pdf 教育文库 教育资源网 新时代文库www Xsdwk Com 教育文库 教育资源网 新时代文库www Xsdwk Com
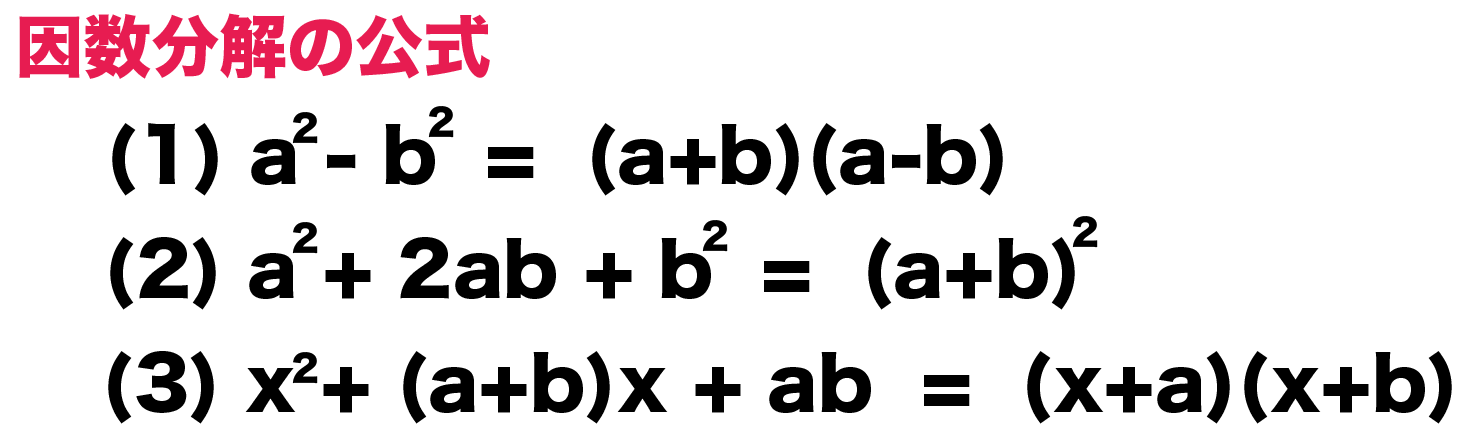



中学数学 因数分解の2つの公式の覚え方 Qikeru 学びを楽しくわかりやすく




圆柱的侧面积公式 圆锥的面积公式 环球信息网



18届河北省衡水中学高三下学期模拟数学试卷理科 8 高考网



三角和积互换六公式 知乎




式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく




乗法公式 多項式の展開公式 の覚え方と使い方 数学fun




一个二项展开式近似计算估值公式的修正 知网百科



刍议数学例题教学的有效策略 杂志论文 福建中学数学




中学数学3年 展開と乗法公式 受験の月



悟空问答 高中数学泰勒展开式如何应用 个回答



xx学年奉化高级中学数学教研组校本研修活动记录表一1700字 范文118



小学数学公式 圆柱体的表面积公式 数学公式 奥数网




M010 中学3年 展開公式 Youtube



资料分析 二项展开式法 事业单位招聘考试网



二项式定理展开式二项式定理经典例题 二项式定理公式大全




一 非整数幂情形下的广义牛顿二项式定理 五五月月的天 博客园



悟空问答 高中数学泰勒展开式如何应用 个回答
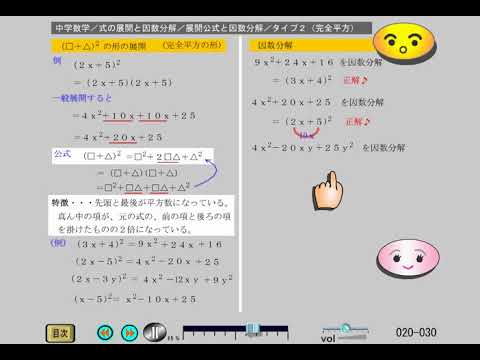



中学数学展開と因数分解 30 公式タイプ2 Youtube



Studydoctor3項式の展開 中3数学 Studydoctor
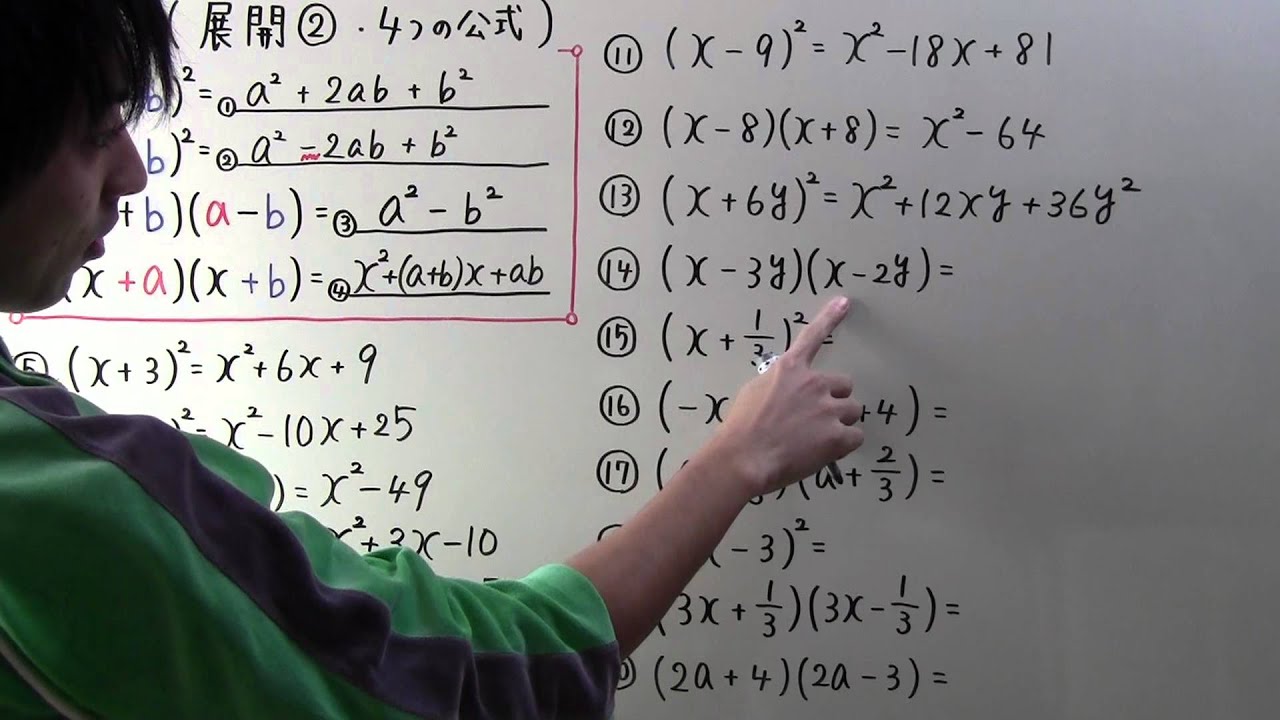



数学 中3 3 展開 4つの公式 Youtube




乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学




用一中学数学公式 中了14次彩票头奖 多国彩票规则因他改变 手机网易网
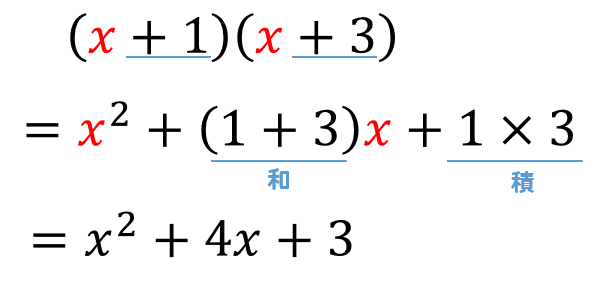



中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ
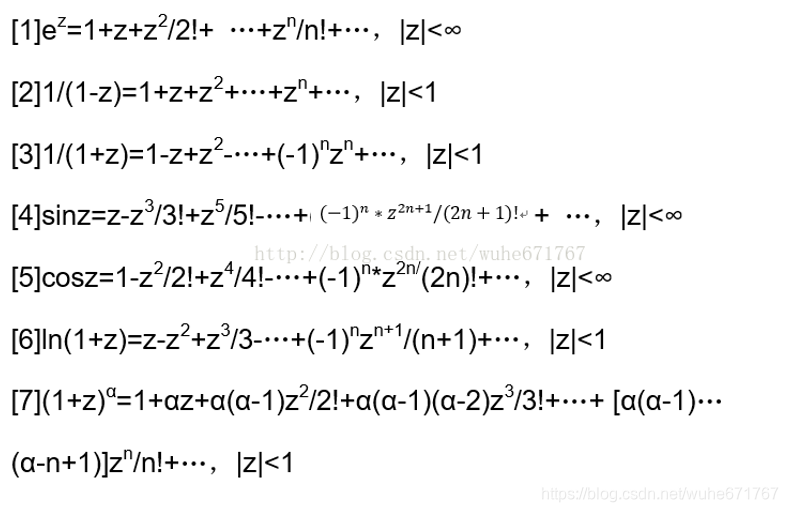



常用泰勒展开 每天的学习笔记 Csdn博客 泰勒公式展开式大全




19 学年4月深圳南山外国语学校 集团 高级中学高二下册月考数学试卷及答案 深圳学而思1对1




高校数学 数 第1章 数と式 3 展開公式 2項の3乗の展開公式 壱のblog




年湖北省荆门市龙泉中学高考数学模拟试卷 理科 3月份 知乎




高中数学基础提升练习 二项式定理 题型练习 知乎
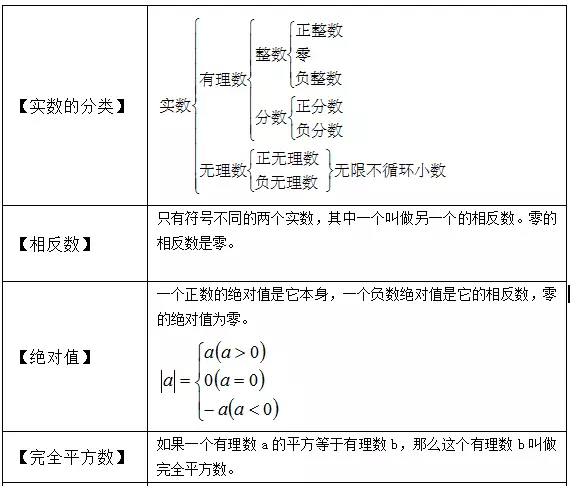



中学数学 初中数学公式定理大汇总 建议收藏



北京一零一中




高校数学の展開公式 さわやか さくらぐみ




函数y 2 X的几种幂级数展开 百度经验




M011 中学3年 展開公式 Youtube




怎样更好地理解并记忆泰勒展开式 知乎




江苏省张家港市后塍高级中学高三数学双周考测试卷下载 Word模板 爱问共享资料




浅谈泰勒公式在高考数学压轴题中的应用 参考网




黑龙江省大庆试验中学09 10学年高二下学期期中考试 数学理 下载 Word模板 爱问共享资料




介绍一个表素数的公式 知乎



北京一零一中




常见函数的泰勒展开式求一些常见初等函数的泰勒展开式



海伦 秦九昭公式的推导与应用例析 自由微信 Freewechat




かずお式中学数学ノート7 中2 式の計算 Amazon Com Books



二项式定理通项公式 搜狗图片搜索



Http Www jdcbs Com Upfile File 03 E6 95 B0 E5 Ad A6 E8 B0 8c E6 A6 E6 96 8c E6 A0 E7 Ab A0 Pdf



21考研 中学数学主要公式总结 Baidu




Jokionasibojedu 0以上展開公式中学 中学3年数学展開公式



数学公式集 無料 中学数学 高校数学の公式解説集 Apk 2 99 6安卓下載 下載数学公式集 無料 中学数学 高校数学の公式解説集 Apk最新版本 Apkfab Com




八年级数学完全平方公式教案下载 Word模板 爱问共享资料




人教版高中数学选修第二册 B版 电子课本



悟空问答 高中数学泰勒展开式如何应用 个回答



21考研 中学数学主要公式总结 Baidu



历年上海中学自主招生试题摘录 上海中考网




分配律英文




積分定数 超算数 は 展開 は私はわからなかった 正解は 乗法 乗法公式 という用語を覚える必要は全くない というのみならず 乗法公式 が特定の4つの式を指すというのも 闇が深い 画像は 数学中学3年教科書 学校図書 平成27年2月




無料ダウンロード数学展開公式 壁紙配布




式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく



怎么给添加的数学公式后面编号 Apple 社区



集团概况教师风采 石家庄外国语教育集团 石家庄外国语学校 石家庄第二外国语学校 石家庄外国语小学 石家庄外国语小学附属双语幼儿园



1 2x的6次方的展开式 西瓜视频搜索




初中三年数学公式定理总结 太有用了 纠错




中学3年数学 3項式の展開 Youtube




高中数学经典解题方法大全 二项式定理三种常见考题精妙解题方法 每日头条




甘肃省武威市第六中学1x 19学年高二数学下学期第二学段考试试题理下载 Word模板 爱问共享资料




高等数学 11 泰勒公式求极限 第三章微分中值定理 每日头条



xx学年奉化高级中学数学教研组校本研修活动记录表一1700字 范文118



二项式定理展开式二项式定理经典例题 二项式定理公式大全




中学数学 多項式 の教え方 展開の応用問題



21考研 中学数学主要公式总结 Baidu




高等数学 11 泰勒公式求极限 第三章微分中值定理 每日头条



左手论文右手代码深入理解网红算法xgboost 开发者头条




中学数学 式の展開 因数分解




年高考数学 理 二轮复习讲练测专题11 排列组合 二项式定理 测 原卷版 Doc 巴士文库
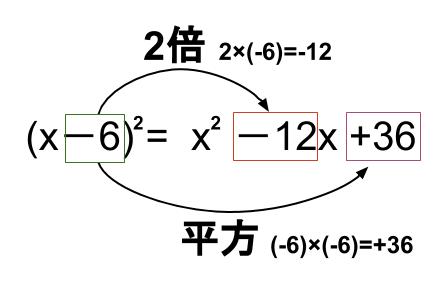



中学数学 式の展開 乗法公式 中学数学の無料オンライン学習サイトchu Su




式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく



幂级数展开式常用公式 幂级数展开式常用公式归纳 Excel教程网



0 件のコメント:
コメントを投稿